Warum ist der Zehnerübergang so schwer und warum scheitern so viele Kinder daran?
In Wahrheit zeigt sich beim Zehnerübergang zum ersten Mal, ob die Grundlagen verstanden wurden. Denn ohne Mengenverständnis, Zahlzerlegung und Zahlaufbau ist der Zehnerübergang ein reines (verstecktes) Zählen.
Außerdem wird hier interessant, dass es nicht nur einen Lösungsweg, sondern viele verschiedene gibt. Das ist wichtig zu wissen, denn dies ist oft die Grundlage für den Streit bei den Hausaufgaben. Die Eltern haben einen anderen Weg im Kopf als das Kind und reden dadurch aneinander vorbei.
Klarer wird es an einem Beispiel:
Die Aufgabe: 6 + 7 =
- Lösungsweg: Bis zur 10 und dann weiter
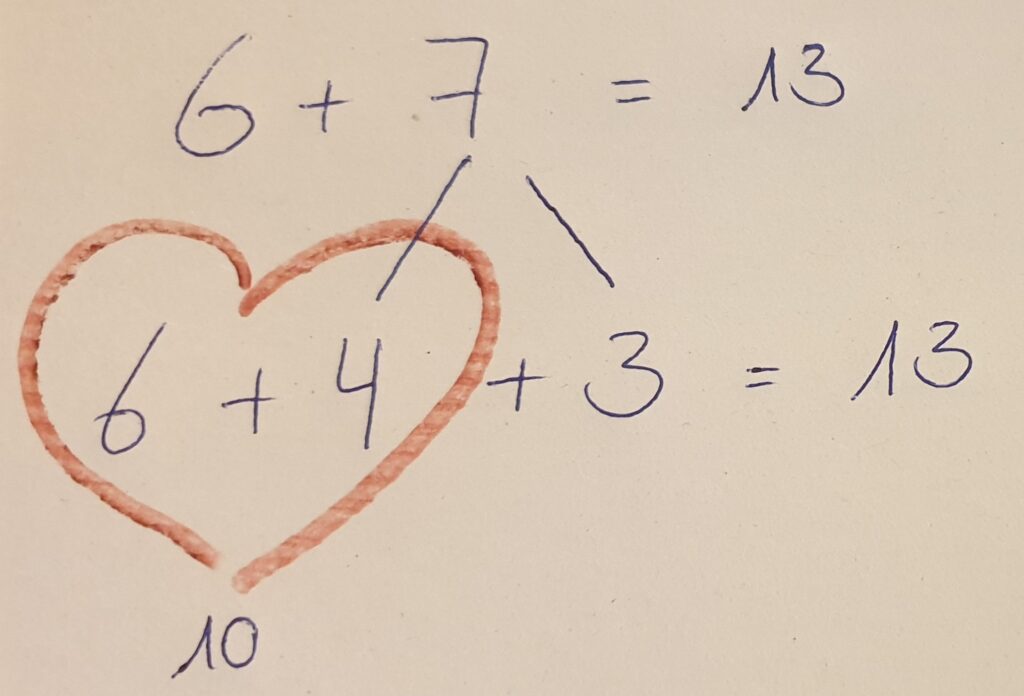
Dies ist die gängigste Lösung und wird in vielen Schulen auch intensiv geübt. Die Kinder rechnen vom 1. Summanden (6) bis zur 10 und überlegen dann, wie viel sie vom zweiten Summanden (7) noch zur 10 addieren müssen.
Die Zahlen 6 und 4 sind deshalb in einem Herzchen zusammengefasst, da es sich um verliebte Zahlen (Zahlen, die zusammenaddiert 10 ergeben) handelt. Dies wird im Vorfeld mit den Schülern intensiv geübt.
Was muss ein Schüler oder eine Schülerin also für die Lösung können?
- Verliebte Zahlen (wie viel fehlt von der ersten Zahl bis zur 10?)
- Zahlzerlegung im Zahlenraum 10 (Wie viel muss ich von der 2. Zahl noch dazurechnen?)
- Grundverständnis der Addition (Mengen werden zusammengefügt oder vereinigt)
- Verständnis des Zehnersystems (Bündelung der Zehner)
Da viele Kinder in den oben genannten Fähigkeiten noch Lücken aufweisen, machen sie viele Fehler, gehen auf Nummer sicher und nehmen den
- Lösungsweg: weiterzählen
Für Kinder, die Lücken in den Grundvorstellungen haben, sei es beim Mengenverständnis, der Zahlzerlegung oder dem Zehneraufbau, bedeutet jede Plusaufgabe einfach weiterzählen:
7, 8, 9, 10, 11, 12, 13
Ich zähle also von 6 noch 7 Zahlen weiter.
Was muss ein Schüler oder eine Schülerin für diese Lösung können?
- Korrektes Zählen im Zahlenraum bis 20
Leider entstehen hier auch viele Fehler. Beispielsweise wird oft die Ziffer des ersten Summanden mitgezählt, also 6, 7, 8, 9, 10, 11, 12. Dadurch entsteht der sogenannte „Minus 1 Fehler“
Dennoch erfordert dieser Lösungsweg wenig Vorkenntnisse oder mathematische Vorstellungen.
- Lösungsweg: Verdopplungsaufgaben
Einigen Kindern liegen Verdopplungsaufgaben sehr. Da die 2 Summanden der Aufgabe nah beieinander liegen können diese auch gut genutzt werden.
Die Kinder rechnen dann:
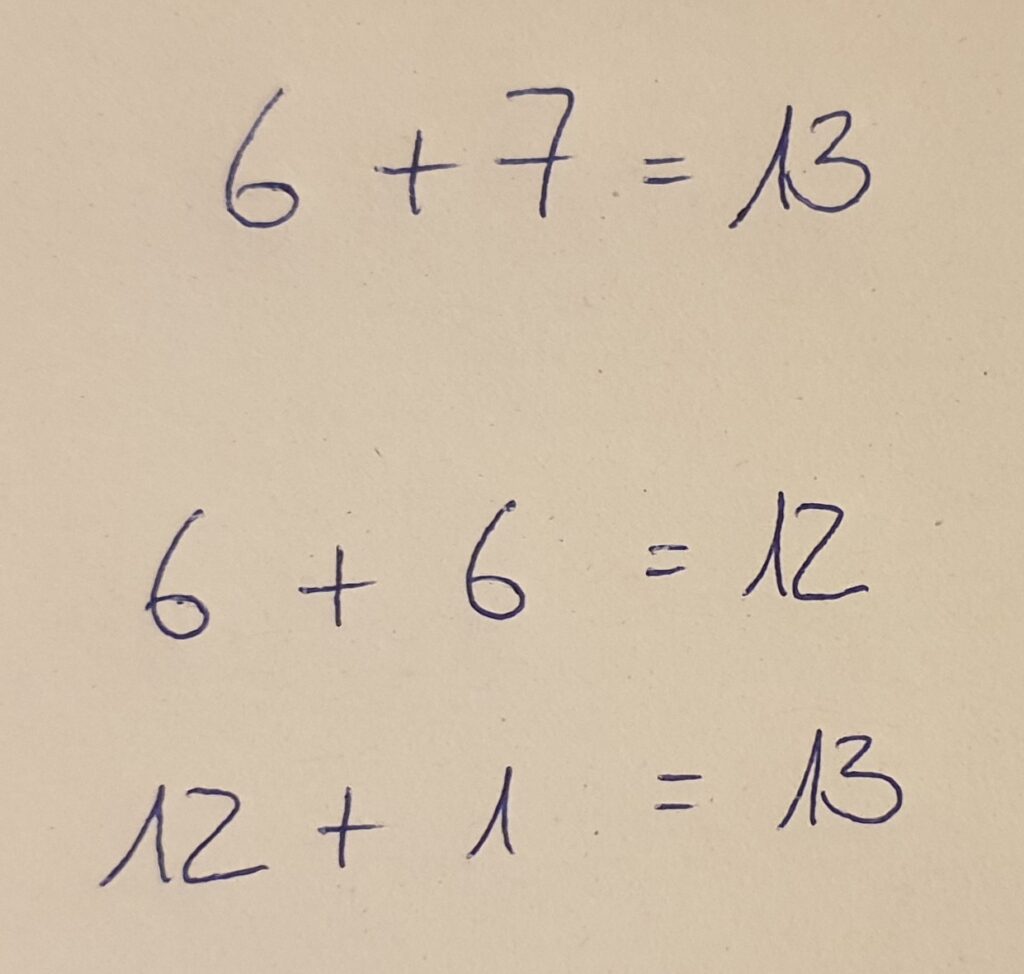
Ebenso verhält es sich, wenn die Kinder 7+7 rechnen und dann 1 abziehen.
Was müssen die Kinder dafür können?
- Verdopplungsaufgaben
- Zahlvorstellung (ich habe nur 6 dazugefügt, fehlt also noch 1) bzw. Zahlzerlegung
Dies waren alles Lösungswege, die auf der Symbolischen Ebene (schriftlich mit Ziffern) und im Kopf gelöst wurden. Man kann aber noch andere Darstellungsformen verwenden
- Lösungsweg: Froschsprünge oder der Rechenstrich
Hier wird ein Rechenstrich zur Visualisierung eingesetzt. Die Froschsprünge entsprechen den Zwischenschritten:
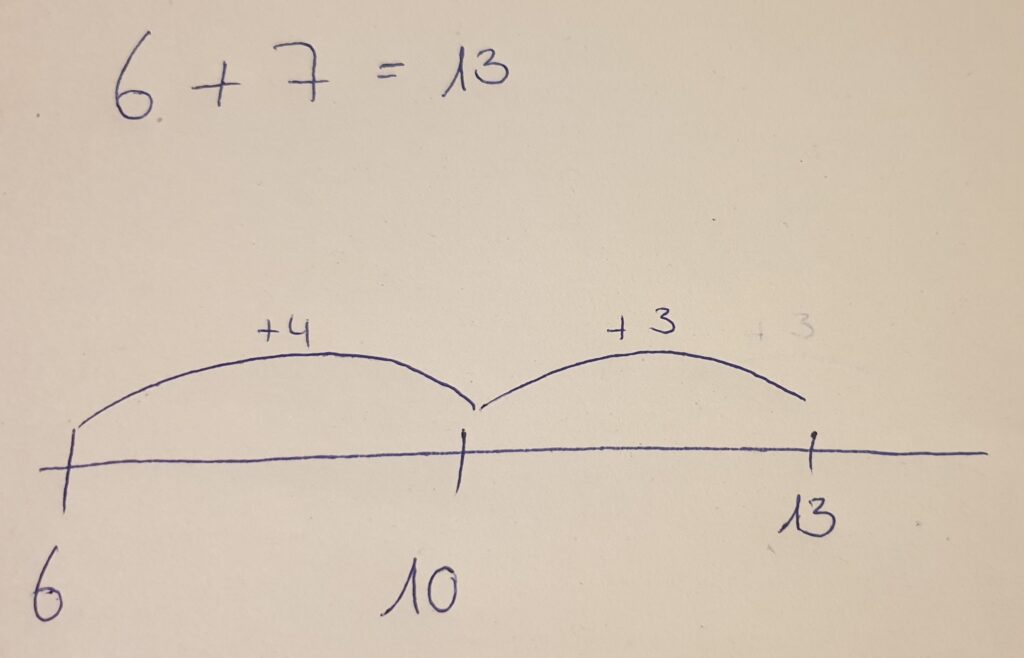
Hier ist der Lösungsweg bis zur 10 und dann weiter dargestellt. Man kann die Sprünge auch entsprechend der Verdopplungsaufgaben oder anderer Einteilungen vornehmen. Der Vorteil liegt darin, dass ich sehe, mit welcher Zahl ich beginne (unten links) und über den Bögen sehe wie viel ich noch zum zweiten Summanden (7) brauche, falls ich mir unsicher bin.
Vorkenntnisse, die zu diesem Lösungsweg notwendig sind:
- Einteilung der Zahlen auf dem Rechenstrich
- Grundvorstellung des Zahlenstrahls
Schüler, die Probleme in Mathematik haben, kommen mit dieser Darstellung sehr schwer zurecht. Ihnen ist nicht klar, dass die Zahlenreihe in gleichen Abständen am Zahlenstrahl vermerkt ist, der dem Rechenstrich zugrunde legt. Sie zeichnen normalerweise die Abstände riesig oder winzig ein, egal welche Zahl sie addieren. Außerdem ist es für Schüler mit wenigen Grundvorstellungen schwer, auf einmal den Rechenstrich bei dem ersten Summanden und nicht bei 0 zu starten. Es ist also kein Weg, der Schülern ohne Grundvorstellungen des Rechenstrichs bei der Lösung hilft, sondern eher verwirrt.
- Lösungsweg: Visuelle Hilfe durch den Abaco oder Zwanzigerkarten
Durch die Einstellung der Zahlen auf dem Abaco oder mit Hilfe der Zwanzigerkarten können beide Summanden auch durch Veranschaulichung zusammengefügt werden.
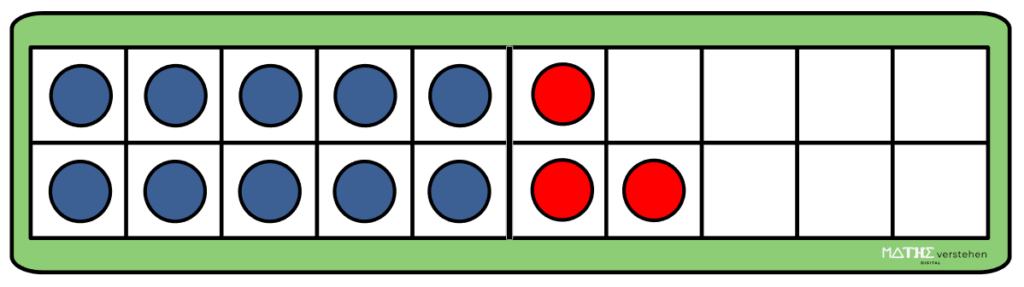
Hier sieht ein Kind beispielsweise die 5 in beiden Summanden und zählt diese als 10 zusammen und addiert im Anschluss noch die 3 einzelnen Punkte bzw. den einen und die beiden übrig gebliebenen.
Diese Darstellung unterstützt das Mengenverständnis und die Kraft der 5. Ist ein Kind an die Kärtchen oder den Abaco gewöhnt, fallen Änderungen im Kopf leicht und verhelfen so zu einem Addieren ohne zu zählen.
Welche Kompetenzen müssen die Kinder hier mitbringen?
- Grundkenntnisse des Materials (Wie stelle ich die Zahl schnell ohne Zählen ein?)
- Umgang mit dem Material (Auffüllen bis zur 10; Zweite Zahl darunter; Punkte im Kopf verschieben, …)
- Lösungsweg: Material
Hier kann jegliches Material zum Legen genommen werden: Legosteine, Bauklötze oder das DINES Material:

Durch die Darstellung und das Handeln mit dem Material wird den Kindern die Bedeutung der Addition („Ich habe 2 Mengen und diese werden zusammengefügt“) deutlich. Wichtig wäre, dass nicht nur abgezählt wird, sondern die einzelnen Summanden übersichtlich („auf einen Blick“) dargestellt und sinnvoll zusammengeführt werden.
- Lösungsweg: Geschichte erzählen
Passend zur Aufgabe kann eine Geschichte erzählt werden, zum Beispiel:
„Im Bus sitzen 6 Personen, es kommen 7 Personen dazu“
Hier wird nochmal das Verständnis der Addition angesprochen. Die Kinder haben ein Bild im Kopf, das ihnen beim Lösen der Aufgabe behilflich sein kann. (Die Personen sitzen zum Beispiel in Zweierreihen, …)
Hier müssen die Kinder folgende Kompetenzen mitbringen:
- Visuelles Vorstellungsvermögen
- Visuelles Operieren (Geschichte im Kopf nachspielen)
- Übersetzen einer Geschichte in eine Mathematikaufgabe / Zuordnung der Angaben zu 1. Summand, 2. Summand und Summe (Ergebnis)
Es gibt noch mehr Lösungswege, dies sind nur diejenigen, die am häufigsten gewählt werden.
Fazit:
Es gibt nicht DEN EINEN Lösungsweg zum Zehnerübergang. Jeder denkt anders, da jeder andere Vorkenntnisse hat, die er nutzt. Man sieht aber sehr gut, dass es unglaublich wichtig ist, beim „Helfen“ erst mal zu fragen:
„Was hast du dir gedacht?“ Oder „Wie hast du gerechnet?“
Dadurch kann man auf das Kind und seinen Weg eingehen und zielgerichtete Hilfestellungen geben. Anderenfalls redet man aneinander vorbei und es entstehen Konflikte, weil keiner den Lösungsweg des anderen versteht.

